ABSTRACT
Zhang (2011)[1] presented improvements to Brent’s method for finding roots of a function of a single variable. Zhang’s improvements make the algorithm simpler and much more understandable. He shows one test example and finds for that case that …
See full abstracts, authors, references, citations & other publication information.
+
…his method converges more rapidly than Brent’s method. There are a few easily-correctible flaws in the algorithm as presented by Zhang which must be corrected in order to implement it. This paper shows these corrections.
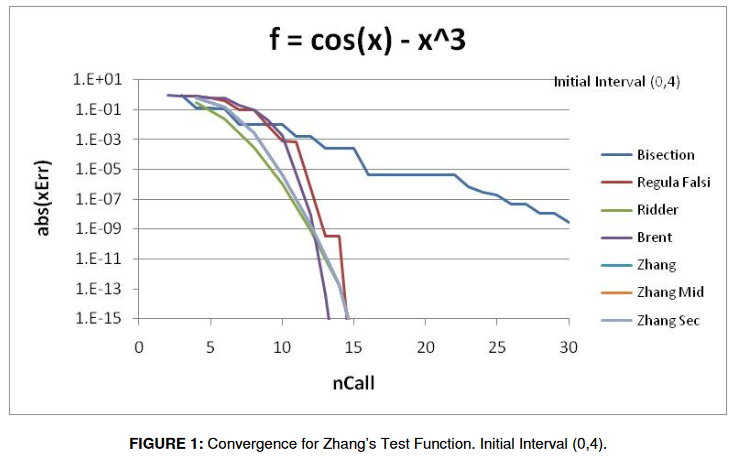
We then proceed to compare the performance of several well-known root finding methods on a number of test functions. Methods tested are Zhang’s method, Bisection, Regula Falsi with the Illinois algorithm, Ridder’s method, and Brent’s method. The results show that Brent’s method and Regula Falsi generally give relatively slow initial convergence followed by very rapid final convergence and that Regula Falsi converges nearly as rapidly as Brent’s method. Zhang’s method and Ridder’s method show similar convergence with both having faster initial convergence than Brent and Regula Falsi but slower final convergence. In many situations, the more rapid initial convergence of the Zhang method and Ridder’s method leads to obtaining solutions with fewer total function evaluations than needed for Brent or Regula Falsi. Selection of the best method depends on the function being evaluated, the size of the initial interval, and the amount of accuracy required for the solution. Large initial intervals and low accuracy favor the Zhang and Ridder methods, while smaller intervals and high accuracy requirements favor Brent and Regula Falsi methods.
Guidance is presented to help the reader determine which root-finding method may be most efficient in a particular situation.
Full Text/Reference Website: https://www.cscjournals.org/library/manuscriptinfo.php?mc=IJEA-33
AUTHORS
Dr. Steven A. Stage – IEM – United States of America
KEYWORDS
Brent’s Method, Zhang’s Method, Ridder’s Method, Regula Falsi Method, Bisection Method, Root Finding, Simplification, Improvement.
Indexing Keywords: Comments on An Improvement to the Brent’s Method, Improvement to the Brent’s Method, Brent’s Method, Brent’s Method Comments, Brent’s Method Improvement.
Pages: 1-16
Revised: 15-01-2013
Published: 28-02-2013Published in International Journal of Experimental Algorithms (IJEA).
Volume: 4
Issue: 1
Publication Date: 28-02-2013
*Randomly selected references used in the publication “Comments on An Improvement to the Brent’s Method”.
- Z. Zhang, An Improvement to the Brent’s Method, IJEA, vol. 2, pp. 21-26, May 31, 2011.
- R.P. Brent. Algorithms for Minimization without Derivatives. Chapter 4. Prentice- Hall,Englewood Cliffs, NJ.
- H.M. Antia. Numerical Methods for Scientists and Engineers, Birkhuser, 2002, pp.362-365, 2 ed.
- W.H. Press, S.A. Teukolsky, W.T. Vetterling and B.P. Flannery. Numerical Recipes in C, The Art of Scientific Computing Second Edition, Cambridge University Press, November 27, 1992, pp.358-362.
- G. Dahlguist and A. Bjorck. Numerical Methods. Dover Publications, 2003, p 232.
CITATIONS
Citations used in the publication “Comments on An Improvement to the Brent’s Method”.
Currently there are no citations collected for this publication at scholarlyabstracts.com.
-
CONTACT US
Please feel free to us at scholarlyabstracts@gmail.com if you wish to:
- Get your journal, conference or thesis, registered with us.
- Update this publication content.
